经典算法详解（10）图中有多少个三角形-白红宇

题目：请说出下面图形中包含多少个三角形？请用一个程序完成计算。

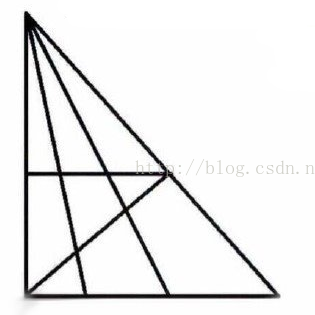
C++版本

1 #include
     
       2  3 using namespace std; 4  5 const char NO_POINT = '0'; 6  7 //任意的一条线 8 const char *map[] = { "ad","ab","db","ae","aj","ah","ej","eh","jh","af","ak","ai","fk","fi","ki","ag","ac","gc", 9 "de","df","dg","ef","eg","fg","bj","bk","bg","jk","jg","kg","bh","bi","bc","hi","hc","ic" };10 //共线的点11 const char *line[] = { "adb","aejh","afki","agc","defg","bjkg","bhic" };12 13 //点是否在线上14 int contain( const char *str, char a) {15     int i = 0;16     while (str[i] != '\0') {        //注意字符使用单引号，字符串是双引号17         if (str[i] == a)18             return 1;19         i++;20     }21     return 0;22 }23 24 //三个点是否在一条线上函数25 int isInALine(const char *str[], char a, char b, char c) {26     int i ;27     for (i = 0; i < 7; i++) {28         if (contain(str[i], a) && contain(str[i], b) && contain(str[i], c)) {29             return 1;30         }31     }32     return 0;33 }34 35 //两条线的交点函数36 char getCrossPoint(const char *str1, const char *str2) {37     if (*str1 == *str2)38         return *str1;39     if (*str1 == *(str2 + 1))40         return *str1;41     if (*(str1 + 1) == *str2)42         return *(str1 + 1);43     if (*(str1 + 1) == *(str2 + 1))44         return *(str1 + 1);45     return NO_POINT;46 }47 48 //三条线两两必须有交点，并且三条线不能共线才能构成三角形。49 int isTriangle(const char *str1, const char *str2, const char *str3) {50     char Point1, Point2, Point3;51     Point1 = getCrossPoint(str1, str2);52     if (Point1 == NO_POINT)53         return 0;54     Point2 = getCrossPoint(str1, str3);55     if (Point2 == NO_POINT)56         return 0;57     Point3 = getCrossPoint(str2, str3);58     if (Point3 == NO_POINT)59         return 0;60     if (isInALine(line, Point1, Point2, Point3))61         return 0;62     return 1;63 }64 65 int getTriangelCount( const char *str[]) {66     int i, j, k,count=0;67     for (i = 0; i < 36; i++) {68         for (j = i+1; j < 36; j++) {69             for (k = j+1; k < 36; k++) {70                 if (isTriangle(str[i], str[j], str[k]))71                     count++;72             }73         }74     }75     return count;76 }77 78 int main(int argc, char *argv[]) {79     cout << getTriangelCount(map);80     getchar();81     return 0;82 }

解题思路：

（1）给每个交点做标记，如下：

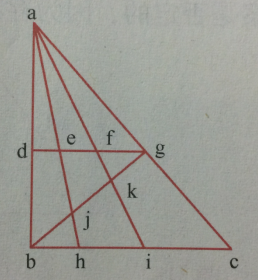
（2）总共有36条线段，如果三条线段两两之间存在交点，但一条线上（已经包含了三条线交于同一点），则可以构成三角形。如下图所示，最左边的构成三角形，右边两个不构成三角形：

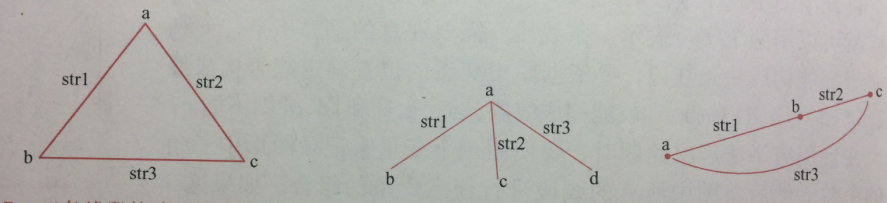
（3）故需要有如下一些子函数：求两条线的交点，三个点是否共线等。